

Similarly we can calculate the LaPlace transform of any derivative of. Note we always end with subtracting a constant term as we run out of initial values at the same time we run out of 's. As the degree of s decreases, the derivative of y (evaluated at 0) increases. The remaining blanks are filled in with initial values, starting with y(0). Thus if we fill in just the first blank in each of the above, we get Note that the coefficient of in Formula 18 is. Lets now fill in the first blank for each of these. Note that if we take the LaPlace transform of the = nth derivative of, we get a degree polynomial. Since, we have that and the initial values are. This is formula 18, though this formula uses instead of : We first need the formula for where is the nth derivative of. Sidenote: FYI if you are given initial values for a nonzero, you can always translate the problem to one where and translate back. To use the LaPlace transform, we need our initial values to be at. We now will use the LaPlace transform to solve an initial value problems.
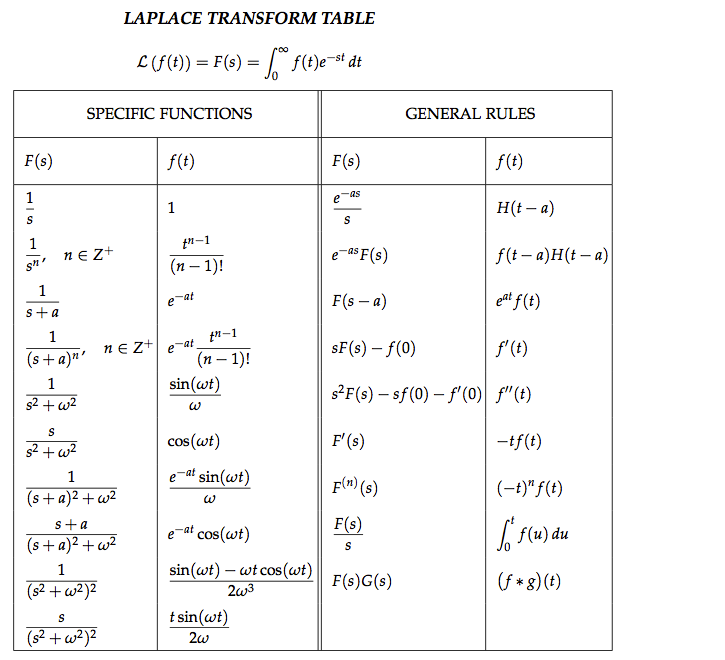
Click on "Show Answers" for helpful information. This example is from Pauls' online notes Section 4-3 : Inverse Laplace Transforms. In your video, include the linearity step. Thus to make it look like the formulas in column 2, you will need use partial fractions. The denominator in this example factors over the reals. Video 18: Ch 6 Inverse LaPlace Transform 9 Thus to make it look like the formulas in column 2, you will need to complete the square. But in this example, the quadratic polynomial has complex roots and thus does not factor over the reals. If it factors over the reals, you will need to use partial fractions. When calculating the inverse LaPlace transform, look at the denominator. Video 16: Ch 6 Inverse LaPlace Transform 7Ĭalculate the inverse LaPlace transform of See Pauls' online notes Section 4-3 : Inverse Laplace Transforms for practice problems including some of the examples below. It takes a lot of work to program a computer to detect patterns and even then computers are not as good as us in most cases (even IF we make more errors). Even if you make lots of algebraic typos (which your professors also do), you are still better than a computer. It might sometime feel like you are not all powerful when it comes to math. $y'' + 3y' + 4y = 0, ~~y(0) = 5, ~~y'(0) = 6$ġ.) Take the LaPlace Transform of both sides of the DE equation:Ģ.) Use the fact that the LaPlace Transform is linear: In chapter 6 we will use the LaPlace transform to turn a linear DE into an algebra problem using linearity and a table of LaPlace transforms. Thus I am copying some of the discussion to this page for an introduction/review of LaPlace transforms. We won't ask you to create videos this semester, but students did much much better than usual on chapter 6 exam problems last year. Last year I created a discussion page asking students to create short video lectures per below. If your browser supports JavaScript, be sure it is enabled. Requires JavaScript to process the mathematics on this page.


 0 kommentar(er)
0 kommentar(er)
